Kepler's equation
Kepler's equation is
 ,
,
where M is the mean anomaly, E is the eccentric anomaly, and 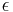 is the eccentricity.
is the eccentricity.
Kepler's equation was first derived by Johannes Kepler in 1619, and has played an important role in the history of both physics and mathematics. It is used to solve problems in orbital mechanics; for specific applications of Kepler's equation, see Kepler's laws of planetary motion.
Contents |
Alternate forms
There are several forms of Kepler's equation. Each form is associated with a specific type of orbit. The standard Kepler equation is used for elliptic orbits (0≤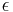 <1). The hyperbolic Kepler equation is used for hyperbolic orbits (
<1). The hyperbolic Kepler equation is used for hyperbolic orbits (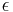 >1). The radial Kepler equation is used for linear (radial) orbits (
>1). The radial Kepler equation is used for linear (radial) orbits (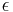 =1). Barker's equation is used for parabolic orbits (
=1). Barker's equation is used for parabolic orbits (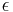 =1). When
=1). When 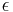 =1, Kepler's equation is not associated with an orbit.
=1, Kepler's equation is not associated with an orbit.
When 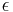 is 0, the orbit is circular. Increasing
is 0, the orbit is circular. Increasing 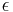 causes the circle to flatten into an ellipse. When
causes the circle to flatten into an ellipse. When 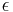 =1, the orbit is completely flat, and it appears to be a either a segment if the orbit is closed, or a ray if the orbit is open. An infinitesimal increase to
=1, the orbit is completely flat, and it appears to be a either a segment if the orbit is closed, or a ray if the orbit is open. An infinitesimal increase to 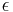 results in a hyperbolic orbit with a turning angle of 180 degrees, and the orbit appears to be a ray. Further increases reduce the turning angle, and as
results in a hyperbolic orbit with a turning angle of 180 degrees, and the orbit appears to be a ray. Further increases reduce the turning angle, and as 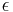 goes to infinity, the orbit becomes a straight line of infinite length.
goes to infinity, the orbit becomes a straight line of infinite length.
Hyperbolic Kepler equation
The Hyperbolic Kepler equation is:
 ,
,
where H is the hyperbolic eccentric anomaly. This equation is derived by multiplying Kepler's equation by the square root of -1, and replacing E with  .
.
Radial Kepler equation
The Radial Kepler equation is:
 ,
,
where t is related to the time, and x is related to the distance. This equation is derived by multiplying Kepler's equation by 1/2, replacing E with  , and setting
, and setting 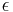 = 1.
= 1.
Inverse problem
Calculating M for a given value of E is straightforward. However, solving for E when M is given can be considerably more challenging.
Kepler's equation is transcendental, which means it cannot be solved for E algebraically. Kepler's equation can be solved for E analytically by Lagrange inversion. The solution of Kepler's equation given by two Taylor series below.
Confusion over the solvability of Kepler's equation has persisted in the literature for four centuries. It is often erroneously claimed that Kepler's equation "cannot be solved analytically".[1] Many authors make the absurd claim that it cannot be solved at all.[2]
The first to make this assertion was Kepler himself:
I am sufficiently satisfied that it [Kepler's equation] cannot be solved a priori, on account of the different nature of the arc and the sine. But if I am mistaken, and any one shall point out the way to me, he will be in my eyes the great Apollonius.
— Johannes Kepler [3]
Inverse Kepler equation
The inverse Kepler equation is the solution of Kepler's equation for all real values of  :
:
![E =
\begin{cases}
\displaystyle \sum_{n=1}^{\infty}
{\frac{M^{\frac{n}{3}}}{n!}} \lim_{\theta \to 0} \left(
\frac{\mathrm{d}^{\,n-1}}{\mathrm{d}\theta^{\,n-1}} \left(
\frac{\theta}{ \sqrt[3]{\theta - \sin(\theta)} } ^n \right)
\right)
, & \epsilon = 1 \\
\displaystyle \sum_{n=1}^{\infty}
{ \frac{ M^n }{ n! } }
\lim_{\theta \to 0} \left(
\frac{\mathrm{d}^{\,n-1}}{\mathrm{d}\theta^{\,n-1}} \left(
\frac{ \theta }{ \theta - \epsilon \cdot \sin(\theta)} ^n \right)
\right)
, & \epsilon \ne 1
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/ac04fa6e35565eef558660fead04c73c.png)
Evaluating this yields:

These series can be reproduced in Mathematica with the InverseSeries operation.
InverseSeries[Series[M - Sin[M], {M, 0, 10}]]InverseSeries[Series[M - e Sin[M], {M, 0, 10}]]
These functions are simple Taylor series. Taylor series representations of transcendental functions are considered to be definitions of those functions. Therefore this solution is a formal definition of the inverse Kepler equation. While this solution is the simplest in a certain mathematical sense, for values of 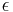 near 1 the convergence is very poor, other solutions are preferable for most applications. Alternatively, Kepler's equation can be solved numerically.
near 1 the convergence is very poor, other solutions are preferable for most applications. Alternatively, Kepler's equation can be solved numerically.
The solution for 
 was discovered by Karl Stumpff in 1968,[4] but its significance wasn't recognized.[5]
was discovered by Karl Stumpff in 1968,[4] but its significance wasn't recognized.[5]
Inverse radial Kepler equation
The inverse radial Kepler equation is:
Evaluating this yields:
To obtain this result using Mathematica:
InverseSeries[Series[ArcSin[Sqrt[t]] - Sqrt[(1 - t) t], {t, 0, 15}]]
See also
- Kepler's laws of planetary motion
- Kepler problem
- Kepler problem in general relativity
- Radial Trajectory
References
- ^ http://www.jgiesen.de/kepler/kepler.html
- ^ M. V. K. Chari, Sheppard Joel Salon 2000 Technology & Engineering
- ^ Kepler's Problem, by Asaph Hall 1883 Annals of Mathematics
- ^ Stumpff, Karl (1968b) On The application of Lie-series to the problems of celestial mechanics, NASA Technical Note D-4460
- ^ Colwell, Peter (1993), Solving Kepler's Equation Over Three Centuries, Willmann-Bell. pg 43.



